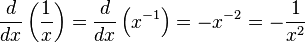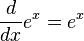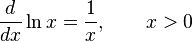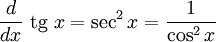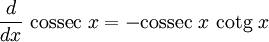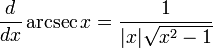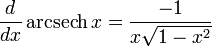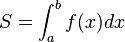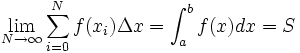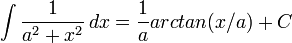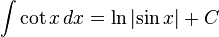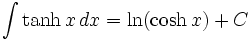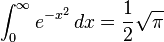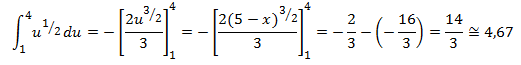FiCaQui: Cálculo Diferencial e Integral

Aqui você aprende conceitos importantes do cálculo.

Teorema Fundamental do Cálculo

É a base das duas operações centrais do cálculo, diferenciação e integração, que são considerados como inversos um do outro. Isto significa que se uma função contínua é primeiramente integrada e depois diferenciada, volta-se na função original. Este teorema é de importância central no cálculo tanto que recebe o nome teorema fundamental para todo o campo de estudo.
Em seu livro de 2003, James Stewart credita a idéia que conduziu ao teorema fundamental ao matemático inglês Isaac Barrow apesar da primeira prova conhecida deste teorema ser reconhecida ao matemático escocês James Gregory. O teorema fundamental do cálculo estabelece a importante conexão entre o Cálculo Diferencial e o Cálculo Integral. O primeiro surgiu a partir do problema de se determinar a reta tangente a uma curva em um ponto, enquanto o segundo surgiu a partir do problema de se encontrar a área de uma figura plana.
Barrow, professor de Newton em Cambridge, descobriu que os dois problemas estão intimamente relacionados, percebendo que os processos de diferenciação e integração são processos inversos. Entretanto, foram Newton e Leibniz, independentemente, que exploraram essa conexão e desenvolveram o Cálculo.
Em particular, eles perceberam que o Teorema Fundamental permitia encontrar a área de uma figura plana de uma forma muito fácil, sem a necessidade de se calcular a soma de áreas de um número indefinidamente grande de retângulos, mas sim usando a primitiva da função envolvida.

O teorema fundamental do cálculo provou que a integração e a diferenciação são processos inversos.
Intuitivamente, o teorema simplesmente diz que a soma de variações infinitesimais em uma quantidade ao longo do tempo (ou ao longo de outra quantidade) adiciona a variação líquida naquela quantidade.

Limite

Limite é usado para descrever o comportamento de uma função à medida que o seu argumento se aproxima de um determinado valor, assim como o comportamento de uma sequência de números reais, à medida que o índice (da sequência) vai crescendo, i.e. tende para infinito. Os limites são usados no cálculo diferencial e em outros ramos da análise matemática para definir derivadas e a continuidade de funções.

O conceito de limite é formalmente é baseado sendo

f

uma função definida num intervalo aberto contendo

a

(excepto possivelmente

a

) e sendo

A

um número real.

Derivada

A derivada representa a taxa de variação de uma função. Um exemplo típico é a função velocidade que representa a taxa de variação (derivada) da função espaço. Do mesmo modo a função aceleração é a derivada da função velocidade.

Diz-se que uma função f é derivável (ou diferenciável) se, próximo de cada ponto a do seu domínio, a função f(x) − f(a) se comportar aproximadamente como uma função linear, ou seja, se o seu gráfico for aproximadamente uma reta. O declive de uma tal reta é a derivada da função f no ponto ae representa-se por

Definição: Considerando um intervalo com mais do que um ponto do conjunto R dos números reais e seja f uma função em R. Se a pertencer a este intervalo, diz-se que f é derivável em a se existir o limite e o mesmo for finito.

A imagem abaixo representa a reta tangente à curva em um ponto, que é a reta que melhor aproxima a vizinhança em um ponto. Ao chegar mais perto do ponto pelos pontos da vizinhança na reta tangente, confunde-se qual é a reta e qual é a curva.

Esta reta é traçada para facilitar a análise da curva próximo ao ponto de tangencia.

A derivada da função em um ponto pode ter duas interpretações:

-Algébricamente é o coeficiente angular da reta tangente à curva em um ponto.
-Fisicamente é a taxa de variação entre duas grandezas.

Quando a função possui derivada ela é continua. Quando o limite da função em um ponto não existe, porque os limites laterais não existem a função não possui derivada nesse ponto.

Derivadas de ordem superior

Quando obtemos a derivada de uma função o resultado é também uma função de x e como tal também pode ser diferenciada. Calculando-se a derivada novamente obtemos então a segunda derivada da função f. De forma semelhante, a derivada da segunda derivada é chamada de terceira derivada e assim por diante. Podemos nos referir às derivadas subsequentes de f por:

$\frac{df}{dx},\quad \frac{d}{dx}\left(\frac{df}{dx}\right),\quad \frac{d}{dx}\left(\frac{d}{dx}\left(\frac{df}{dx}\right)\right)$

e assim sucessivamente. No entanto, a notação mais empregada é:

$\frac{df}{dx},\quad \frac{d^{2}f}{dx^2},\quad \frac{d^{3}f}{dx^3}$

ou alternativamente,

$f'(x),\quad f''(x),\quad f'''(x)$

Pontos Críticos

Ponto onde a derivada da função não existe ou é igual a 0. Estes pontos acontecem onde a reta tangente é paralela ao eixo dos

x

. O coeficiente da reta tangente é igual a 0.

Estes pontos podem acontecer:

onde a função atinge um valor máximo e depois começa a diminuir, chamados máximos locais da função
onde ela atinge um valor mínimo e começa a aumentar, chamados de mínimos locais da função
onde existem os pontos de inflexão da função, que são definidos como os pontos onde a concavidade da função muda.

Máximos e Mínimos

Para determinar se possuimos um máximo e um mínimo deve-se:

calcular a derivada
verificar os números críticos que são encontrados igualando a derivada a 0.
estudar o sinal da derivada.

Para estudar o comportamento da função

Analisando a primeira derivada
Onde a primeira derivada é positiva a função é crescente.
Onde a primeira derivada é negativa a função é decrescente.
Onde a primeira derivada é igual a 0 a função é constante.

Analisando a segunda derivada
Onde a segunda derivada é negativa a função possui um máximo local neste ponto.
Onde a segunda derivada é positiva a função possui um mínimo local neste ponto.

Onde a segunda derivada é positiva o gráfico da função função é côncavo para cima
Onde a segunda derivada é negativa o gráfico da função é côncavo para baixo.

Regras de derivação

Regra do Produto

Regra do Quociente

Regra da Cadeia

A regra fica mais simples de entender por este exemplo:

f (x) = (x 2 + 1) 3

Derivada de função implícita

São funções onde não temos de um modo explicito uma relação entre as duas variáveis pela qual possamos escrever

y = f (x)

como exemplo a função:

y 2 + x 2 = 1

Deriva-se a função em relação a x

Aplica-se a regra da cadeia para derivar o y

Deriva o restante normalmente

Isolamos o quociente de diferenciais que representa a derivada

Simplifica-se para obter a derivada.

Tabela de derivadas

Para você que faz um curso que possui cálculo na grade curricular é extremamente útil possuir uma tabela com as regras de derivação à mão. Pois não é necessário decorá-las e sim entendê-las.

Derivadas de funções simples

${d \over dx} c = 0$

${d \over dx} x = 1$

${d \over dx} cx = c$

${d \over dx} |x| = {|x| \over x} = \sgn x,\qquad x \ne 0$

${d \over dx} x^c = cx^{c-1} \qquad \mbox{ onde tanto } x^c \mbox{ quanto } cx^{c-1} \mbox{ são definidos}$

${d \over dx} \left({1 \over x}\right) = {d \over dx} \left(x^{-1}\right) = -x^{-2} = -{1 \over x^2}$

${d \over dx} \left({1 \over x^c}\right) = {d \over dx} \left(x^{-c}\right) = -{c \over x^{c+1}}$

${d \over dx} \sqrt{x} = {d \over dx} x^{1\over 2} = {1 \over 2} x^{-{1\over 2}} = {1 \over 2 \sqrt{x}}, \qquad x > 0$

Derivadas de funções exponenciais e logarítmicas

${d \over dx} c^x = {c^x \ln c },\qquad c > 0$

${d \over dx} e^x = e^x$

${d \over dx} \log_c x = {1 \over x \ln c},\qquad c > 0, c \ne 1$

${d \over dx} \ln x = {1 \over x},\qquad x > 0$

${d \over dx} \ln |x| = {1 \over x}$

${d \over dx} x^x = x^x(1+\ln x)$

Derivadas de funções trigonométricas

${d \over dx} \mbox{ sen } x = \cos x$

${d \over dx} \cos x = -\mbox{sen } x$

${d \over dx} \mbox{ tg } x = \sec^2 x = { 1 \over \cos^2 x}$

${d \over dx} \sec x = \mbox{ tg } x \sec x$

${d \over dx} \mbox{ cotg } x = -\mbox{cossec }^2 x = { -1 \over \mbox{sen}^2 x}$

${d \over dx} \mbox{ cossec } x = -\mbox{cossec } x \mbox{ cotg } x$

${d \over dx} \mbox{ arcsen } x = { 1 \over \sqrt{1 - x^2}}$

${d \over dx} \arccos x = {-1 \over \sqrt{1 - x^2}}$

${d \over dx} \mbox{ arctg } x = { 1 \over 1 + x^2}$

${d \over dx} \arcsec x = { 1 \over |x|\sqrt{x^2 - 1}}$

${d \over dx} \mbox{ arccotg } x = {-1 \over 1 + x^2}$

${d \over dx} \mbox{ arccossec } x = {-1 \over |x|\sqrt{x^2 - 1}}$

Derivadas de funções hiperbólicas

${d \over dx} \mbox{ senh } x = \cosh x = \frac{e^x + e^{-x}}{2}$

${d \over dx} \cosh x = \mbox{ senh } x = \frac{e^x - e^{-x}}{2}$

${d \over dx} \mbox{ tgh } x = \mbox{sech}^2\,x$

${d \over dx}\,\mbox{ sech }\,x = - \mbox{ tgh } x\,\mbox{ sech }\,x$

${d \over dx}\,\mbox{ cotgh }\,x = -\,\mbox{ cossech}^2\,x$

${d \over dx}\,\operatorname{csch}\,x = -\,\operatorname{coth}\,x\,\operatorname{cossech}\,x$

${d \over dx}\,\operatorname{arcsinh}\,x = { 1 \over \sqrt{x^2 + 1}}$

${d \over dx}\,\operatorname{arccosh}\,x = { 1 \over \sqrt{x^2 - 1}}$

${d \over dx}\,\operatorname{arctanh}\,x = { 1 \over 1 - x^2}$

${d \over dx}\,\operatorname{arcsech}\,x = { -1 \over x\sqrt{1 - x^2}}$

${d \over dx}\,\operatorname{arccoth}\,x = { 1 \over 1 - x^2}$

${d \over dx}\,\operatorname{arccossech}\,x = {-1 \over |x|\sqrt{1 + x^2}}$

Integral

A integral de uma função foi criada originalmente para determinar a área sob a curva no plano cartesiano e tmbém surge naturalmente em dezenas de outros problemas.

A integral também é conhecida como antiderivada

Para se descrever a integral de uma função f de uma variável x entre o intervalo [a, b] utiliza-se a notação:

$S = \int_{a}^{b} f(x) dx$

A integral de f(x) pode ser entendida como a soma de pequenos retângulos de base dx tendendo a zero e altura f(x), onde o produto f(x) dx é a área deste retângulo. A soma de todas estas pequenas áreas, ou áreas infinitesimais, fornece a área total abaixo da curva. Mais precisamente, pode-se dizer que a integral acima é o valor limite da soma:

$\sum_{i=0}^{N} f(x_i) \Delta x.$

onde:

$\Delta x = \frac{b-a}{N}$

é o comprimento dos pequenos intervalos nos quais se divide o intervalo (b-a),

f (x i)

é o valor da função em algum ponto deste intervalo. O que se espera é que quando N for muito grande o valor da soma acima se aproxime do valor da área abaixo da curva e, portanto, da integral de f(x) no intervalo. Ou seja, que o limite

$\lim_{N\to\infty} \sum_{i=0}^{N} f(x_i) \Delta x = \int_{a}^{b} f(x) dx = S$

esteja definido. O problema é que este raciocínio intuitivo é difícil de colocar em linguagem matemática precisa. Por isto existem várias formas de se definir a integração de maneira formal. O resultado entretanto é coerente entre elas.

O símbolo da integral, ou o "s espichado" é utilizado dessa maneira para denotar uma soma

Como calcular uma integral?

Integral Definida - Uma integral definida consta basicamente em integrar uma função constante nos intervalos, através das primitivas, que nada mais são do que a função integrada a cada membro. Basta seguir a fórmula:

$\int a\cdot x^{n} dx = \frac{a\cdot x^{n+1}} {n+1}$

Fica mais fácil compreender observando um exemplo:

No intervalo (0,3)

f (x) = x 2 + 2 x + 4

$\int x^{2} dx + \int (2x) dx + \int (4) dx$

Aqui usa-se a Fórmula da Primitiva em cada integral.

$\frac{x^{2+1}} {2+1} + \frac{2\cdot x^{1+1}} {1+1} + \frac{4 \cdot x^{0+1}} {0+1}$

Gera-se a outra função, que será usada para substituir os valores do intervalo.

$\frac{x^3} {3} + x^2 + 4\cdot x$

Para x = 0

f (a) = 0

Para x = 3

$\frac{3^3} {3} + 3^2 + 4\cdot 3$

f (b) = 30

Tábua de Integrais

Propriedades da Integral Indefinida

$\int cf(x)\,dx = c\int f(x)\,dx$

$\int [f(x) + g(x)]\,dx = \int f(x)\,dx - \int g(x)\,dx$

$\int f(x)g(x)\,dx = f(x)\int g(x)\,dx + \int \left(d[f(x)]\int g(x)\,dx\right)dx$ ou, de outra forma,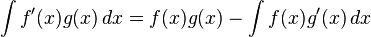

$\int f'(x)g(x)\,dx = f(x)g(x) - \int f(x)g'(x)\,dx$

Integrais Indefinidas de Funções Simples

$\int x^n\,dx = \frac{x^{n+1}}{n+1} + C\qquad\mbox{ para }n \ne -1$

$\int \frac{1}{x}\,dx = \ln{\left|x\right|} + C$

$\int \frac{1}{a^2+x^2} \, dx = \frac{1} {a} arctan({x}/{a}) + C$

Logaritmos

$\int \log_a x\,dx = x\log_a x - \frac{x}{\log a} + C$

$\int \ln x\,dx = x \ln x - x + C$

Funções Exponenciais

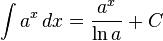
$\int a^x\,dx = \frac{a^x}{\ln{a}} + C$

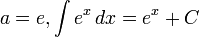
Caso particular: $a = e, \int e^x\,dx = e^x + C$

Funções Irracionais

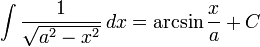
$\int {1 \over \sqrt{a^2-x^2}} \, dx = \arcsin {\frac{x}{a}} + C$

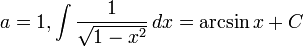
Caso particular: $a = 1, \int {1 \over \sqrt{1-x^2}}\, dx = \arcsin {x} + C$

$\int {-1 \over \sqrt{a^2-x^2}} \, dx = \arccos {\frac{x}{a}} + C = (-1)arcsin {\frac{x}{a}} + C$

Caso particular: $a = 1, \int {-1 \over \sqrt{1-x^2}} \, dx = \arccos {x} + C$

Funções Trigonométricas

$\int \cos{x} \, dx = \sin{x} + C$

$\int \sin{x} \, dx = -\cos{x} + C$

$\int \tan{x} \, dx = -\ln{\left| \cos {x} \right|} + C$

$\int \csc{x} \, dx = \ln{\left| \csc{x} - \cot{x}\right|} + C$

$\int \sec{x} \, dx = \ln{\left| \sec{x} + \tan{x}\right|} + C$

$\int \cot{x} \, dx = \ln{\left| \sin{x} \right|} + C$

$\int \sec{x} \tan{x} \, dx = \sec {x} + C$

$\int \csc{x} \cot{x} \, dx = -\csc {x} + C$

$\int \sec^2 x \, dx = \tan x + C$

$\int \csc^2 x \, dx = -\cot x + C$

$\int \sin^2 x \, dx = \frac{1}{2}(x - \sin x \cos x) + C$

$\int \cos^2 x \, dx = \frac{1}{2}(x + \sin x \cos x) + C$

Funções Hiperbólicas

$\int \sinh x \, dx = \cosh x + C$

$\int \cosh x \, dx = \sinh x + C$

$\int \tanh x \, dx = \ln (\cosh x) + C$

$\int \mbox{csch}\,x \, dx = \ln\left| \tanh {x \over2}\right| + C$

$\int \mbox{sech}\,x \, dx = \arctan(\sinh x) + C = \arcsin(\tanh(x)) + C = 2\arctan(\exp(x)) + C$

$\int \coth x \, dx = \ln|\sinh x| + C$

Integrais Impróprias

Existem funções cujas antiderivadas não podem ser expressas de forma fechada. No entanto, os valores das integrais definidas dessas funções em intervalos comuns podem ser calculados. Algumas integrais definidas de uso frequente estão relacionadas abaixo.

$\int_0^\infty{\sqrt{x}\,e^{-x}\,dx} = \frac{1}{2}\sqrt \pi$

$\int_0^\infty{e^{-x^2}\,dx} = \frac{1}{2}\sqrt \pi$

$\int_0^\infty{\frac{x}{e^x-1}\,dx} = \frac{\pi^2}{6}$

$\int_0^\infty{\frac{x^3}{e^x-1}\,dx} = \frac{\pi^4}{15}$

$\int_0^\infty\frac{\sin(x)}{x}\,dx=\frac{\pi}{2}$

Exercícios propostos e suas respectivas resoluções:

Limites:

1º)Quando substituímos -3, na equação que define a função, obtemos uma indeterminação.

2º)Quando nos aproximamos de -3 pela esquerda, por valores menores que -3, obtemos valores cada vez maiores negativos, logo 1 dividido por um número muito grande negativo, resulta em -infinito .

Derivadas:

Integral: